Universe Sandbox now realistically simulates the speeds at which clouds rotate.

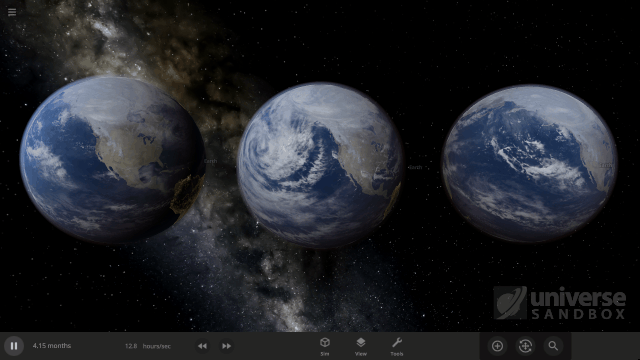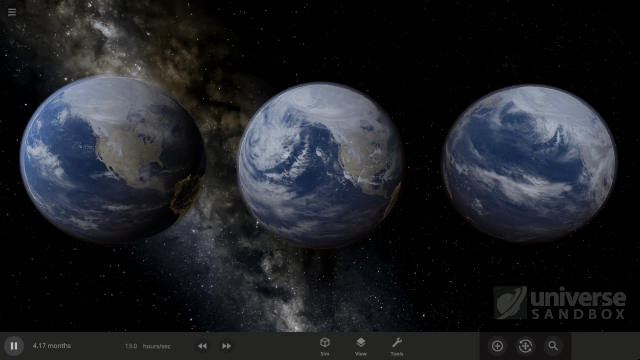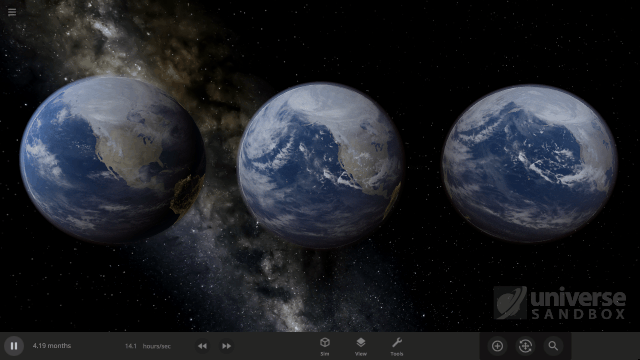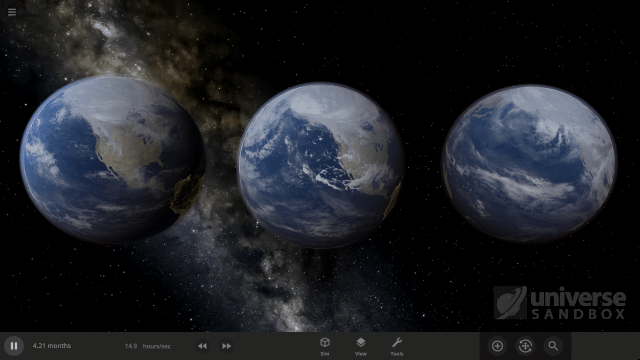
One of our recent improvements to Universe Sandbox includes realistically simulating the speed at which clouds rotate around objects, like planets and moons. While our in-game guide, which can be found under Guides > Science > Clouds, shows off these new features, we wanted to explain them in a little more depth.

To simulate completely realistic clouds, we would need to do a full weather simulation, including the water cycle. As we talk about in our Snow Simulation ScienceLog, this isn’t currently possible without a supercomputer, so for now our clouds are drawn from pre-made cloud pictures. However, we determine the speed at which clouds rotate around an object’s surface from two simulated effects.

Simulating realistic weather patterns faster than real time (one second per second) is very difficult, especially with your average computer.

Creating Wind

In reality wind is initially created going in an unexpected direction – it travels outwards from the equator to the poles instead of rotating around the equator.

This is because objects are (generally) warmer at their equator and colder at their poles. The higher temperatures at the equator lead to a higher air pressure (essentially the weight of the atmosphere) at the equator, while colder temperatures at the poles lead to lower air pressure. The high pressure air at the equator moves to the lower pressure air at the poles, creating a wind that moves the clouds with it.

This wind moves faster, increasing the cloud speed, the larger the temperature difference between the equator and the poles is, since this will create a larger air pressure difference. In Universe Sandbox we simulate this difference in air pressure between an object’s equator and its poles based on the difference between its Minimum and Maximum Temperature, which are usually at the poles and equator.

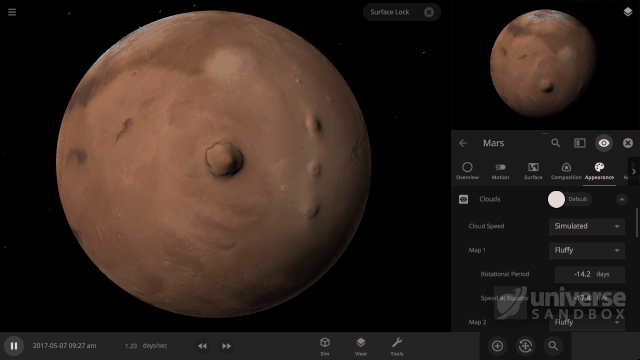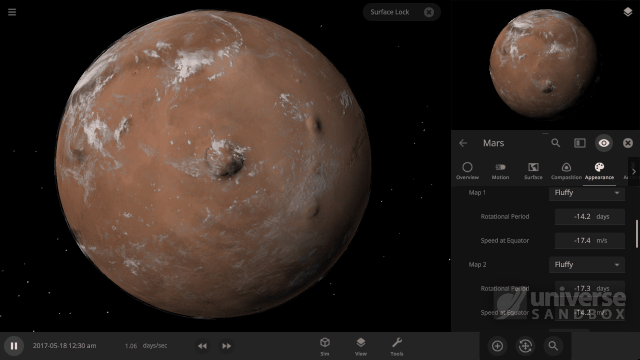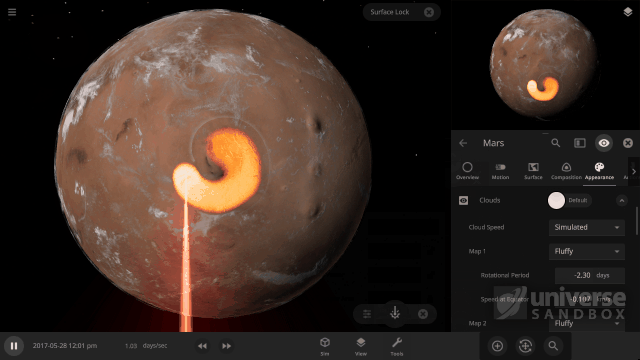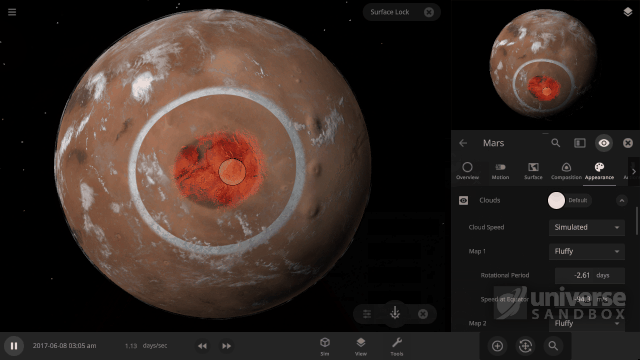
By lasering Mars, we are increasing the maximum temperature, which increases the difference between the maximum and minimum temperatures on Mars, as well as the difference between maximum and minimum air pressures, which increases the cloud speed.

Changing the Wind’s Direction

So if wind, and clouds, starts out moving from the equator to the poles, why is it that in reality (and in Universe Sandbox) the wind and clouds move around the Earth’s equator?

This has to do with something called the Coriolis effect – the second effect we simulate for our cloud rotation speeds – which is an effect that occurs on any object that rotates. The Coriolis effect creates a force, called the Coriolis force, that pushes the wind around the Earth’s (or any object’s) equator. The strength of this force increases the faster the object is rotating.

The Resulting Rotation (Speed)

So we now have two effects pushing the winds, and thus clouds, in two different directions:

  1. The difference in air pressure (and temperature) between the equator and the poles of the object forces the winds to move outwards from the equator to the poles.
  2. The Coriolis Effect pushes the winds around the equator of an object.

So how do we arrive at the final wind, and cloud, rotation speed? The wind speed will increase until the strength of both effects on the wind is the same. When this happens, the wind and clouds end up rotating around the equator of the object at a constant, unchanging speed. In Universe Sandbox this speed is taken as the Cloud Rotation Speed.

Manipulating the Winds

A really interesting effect that happens when our two simulated effects have the same strength is that the faster an object rotates, the slower the cloud speed will be.

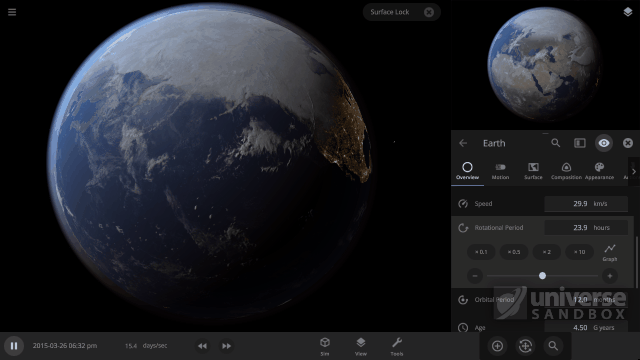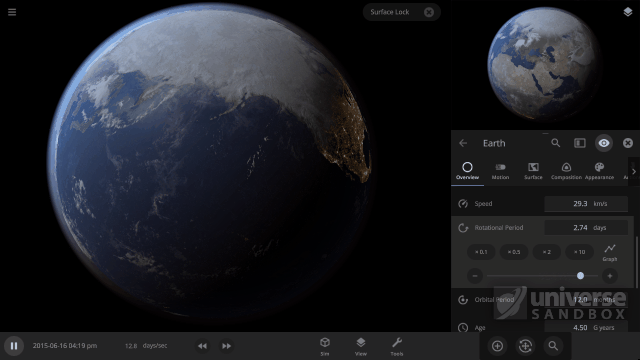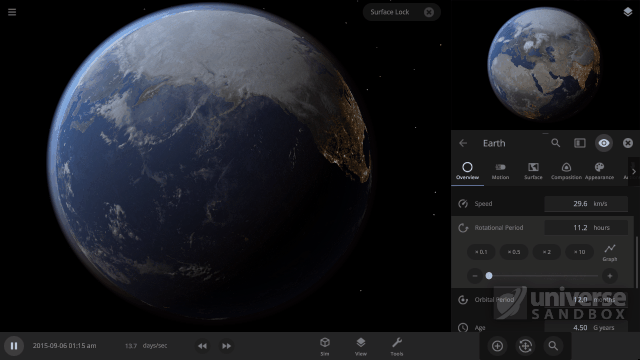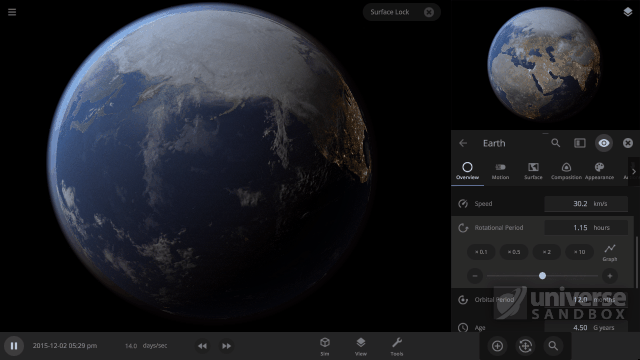
The cloud rotation speed here is changing only based on the rotation speed of Earth. Slower planet rotation speeds lead to faster cloud rotation speeds, which is not what you’d expect at first.

A faster object Rotation Speed creates a stronger force from the Coriolis effect, which allows the two effects to reach an equal strength more quickly. This means that the wind speed has less time to increase before it becomes constant. The result is that the final wind, and Cloud Rotation Speed, is slower.

In addition to Rotation Speed and the Minimum and Maximum Temperature, the strength of the wind that is created from the temperature difference also depends on the Atmosphere Mass, the Surface Gravity, and the Radius of the object (see the Bonus Math section below for details). This is because a more massive atmosphere will slow down the Cloud Rotation Speed, since it is harder to move, and a smaller object radius will increase the Cloud Rotation Speed, since it is easier to move air around a smaller object.

While simulating these effects is a welcomed advancement in our cloud simulation, there are still many improvements we would like to make. This includes dynamically generating clouds and giving them more realistic material compositions. For now, try experimenting with different object properties to see how they affect the Cloud Rotation Speed. We recommend the object’s Rotation Speed, since we can’t slow down the Earth in real life (nor would we want to), this is a great way to see some amazing science at work!

This blog post is part of our ongoing series of ScienceLog articles, intended to share the science behind some of Universe Sandbox’s most interesting features. If you would love to learn about the real-life science powering our simulator, please stay tuned and let us know what you would like to read about next.

To join our community discussions, please join us on our Steam Forum and our official Discord community.

Bonus Math

If you’re interested in exactly how different object properties relate to both the force from the difference in the air pressure between the equator and the poles (called the pressure gradient) and the force from the Coriolis effect (called the Coriolis force) then you’ll enjoy this extra little bit of math. 

When we simulate the cloud rotation speed we figure out the pressure difference, ΔP, which is based on the maximum atmosphere surface pressure, Pmax. This is the surface pressure at the equator, and depends on the Atmosphere Mass, M, the Surface Gravity, g, and the radius of the planet, R,

P_{\rm{max}} = Mg/(4 \pi R^{2}).

The pressure and temperature of a gas are related (by something called the Ideal Gas Law), so we can compute ΔP using just Pmax and the maximum and minimum temperature, Tmax and  Tmin , of the object,

\Delta P = P_{\rm{max}} \left(\frac{T_{\rm{max}}}{T_{\rm{min}}} - 1 \right).

Now that we have this pressure difference, we can compute the force, F, that this pressure gradient applies over a certain amount of air mass, m. This force per mass is what causes winds and clouds to move and depends on ΔP (and a few other less important things). That means that this force can change depending on M, g, R, Tmax and  Tmin , (that is Atmosphere Mass, Surface Gravity, Radius, Maximum Temperature, and Minimum Temperature respectively) so all of these properties affect the cloud rotation speed,

\frac{F}{m} \propto \Delta P \propto P_{\rm{max}} \times \frac{T_{\rm{max}}}{T_{\rm{min}}} \propto 
 \frac{Mg}{R^{2}} \times \frac{T_{\rm{max}}}{T_{\rm{min}}}.

Here the ∝ symbol means “proportional to,” which is similar to an equals sign, “=”, but leaves out some of the less important values. The Coriolis Force also provides a force per mass in order to move clouds. This force is dependent on a few different things, but in particular it depends on the rotation speed of the planet, Ω, and the speed that the wind is already moving due to the pressure gradient, v,

\frac{F}{m} \propto \Omega v.

To reach a balanced state where the wind, and clouds, are moving around the equator of an object at a constant speed, the two forces must be equal, leading to the relationship

\Omega v \propto  \frac{Mg}{R^{2}} \times \frac{T_{\rm{max}}}{T_{\rm{min}}}.

Now the value we want is the wind, or cloud, rotation speed, v. Rearranging the above equation gives us

v \propto \frac{Mg}{\Omega R^{2}} \times \frac{T_{\rm{max}}}{T_{\rm{min}}}.

So what does this mean? First, the larger the difference between the minimum and maximum temperature, the faster the clouds will move. This is because a larger temperature difference means a larger pressure difference, thus faster winds. 

It also shows mathematically why a more massive atmosphere slows the cloud rotation speed and a smaller radius can dramatically increase the cloud rotation speed like we discussed above.

But the most interesting consequence of this relationship is that it shows why it is that the faster an object rotates, the slower the cloud speed will be. This result was so surprising to us at first that we had to triple check it (we’re convinced it is correct now, don’t worry). While it’s impossible to slow down the Earth’s rotation in reality (not to mention the immense destruction that would cause if we could), exploring in Universe Sandbox allows you to see the consequences of some beautiful math for yourself.