The End of the World: Slower Than You Expected | ScienceLog #3

Sure, the Sun’s pretty useful, we guess. It feeds Earth’s plant life, keeps us warm, and helps people see where they’re going when they walk around outside. If the Sun suddenly disappeared from the Solar System (which you can do with the click of a button in Universe Sandbox!), we’d be in big trouble.* In fact, right now you’re probably imagining the desolate, frozen landscape that our planet would become without its Sun. But this apocalypse wouldn’t happen quite as fast as you probably think:

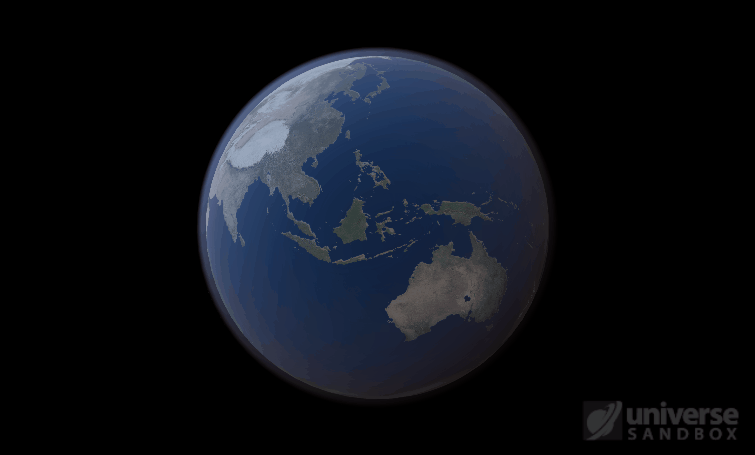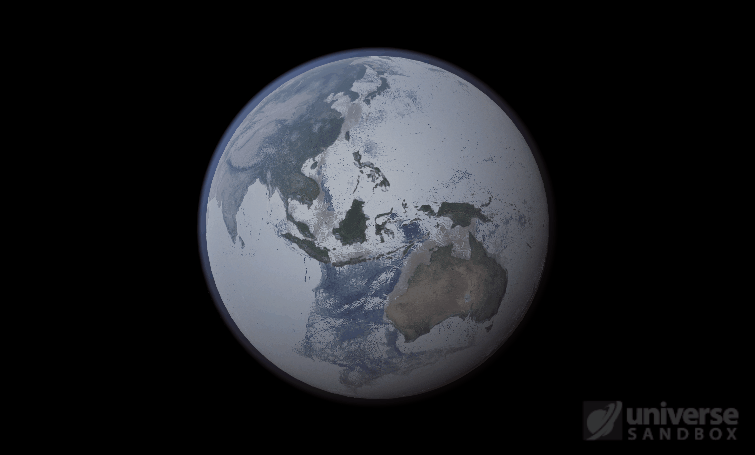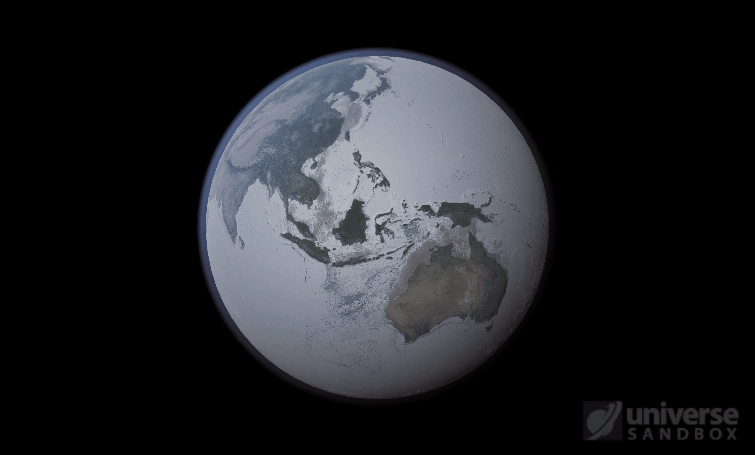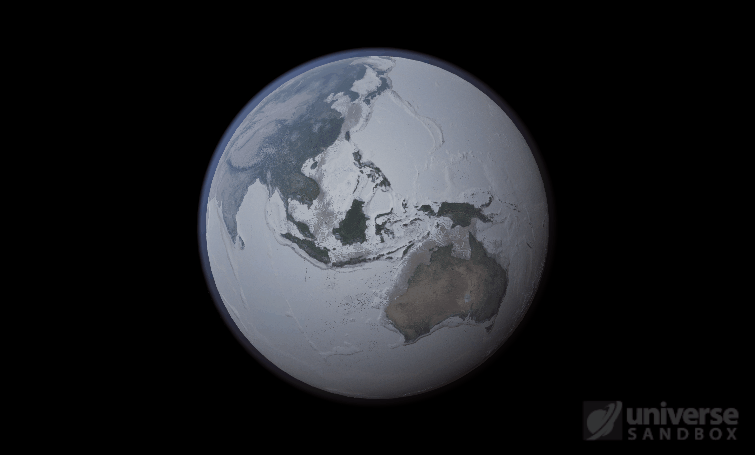
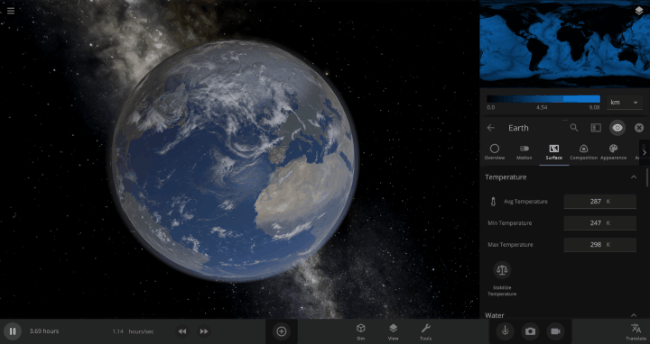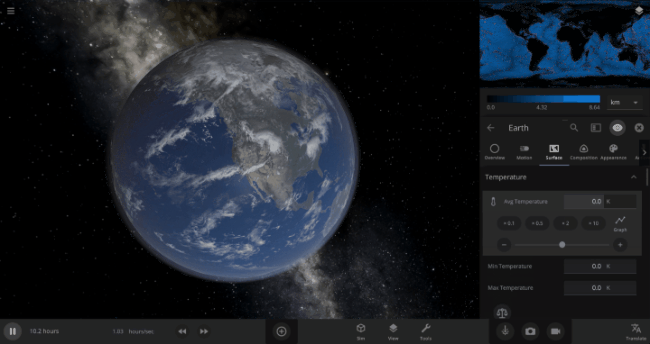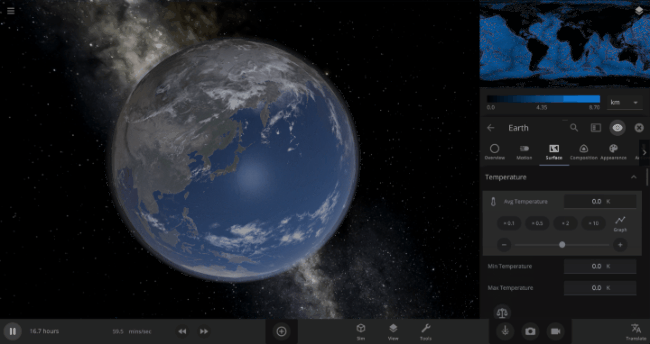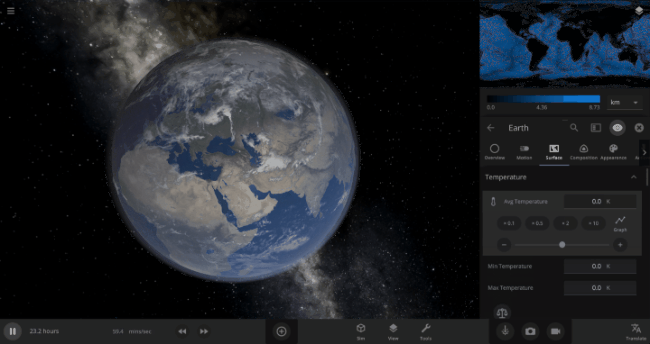
If the Sun disappeared, it would take over a century for the Earth’s oceans to completely freeze solid! 

Universe Sandbox lets you perform this kind of catastrophic experiment from the safety and comfort of your own home by simulating three phases of water (solid, liquid, and gas), and how they react to the changing environment. As a planet cools, its surface water will freeze into ice. Heat that planet back up with a laser, and the ice will melt and even vaporize into gas.

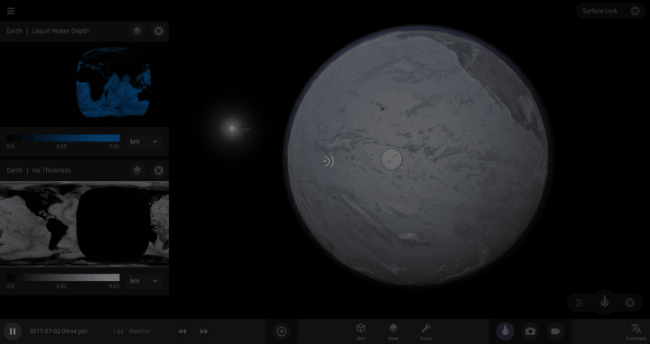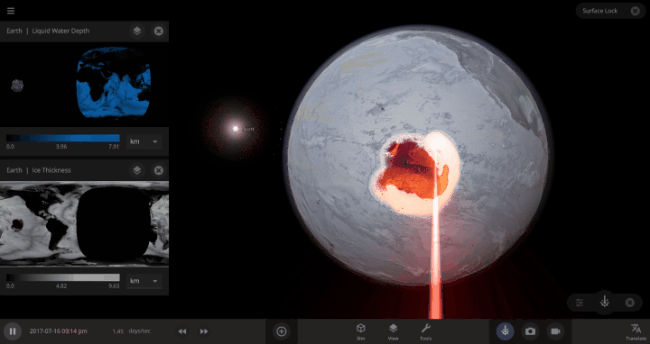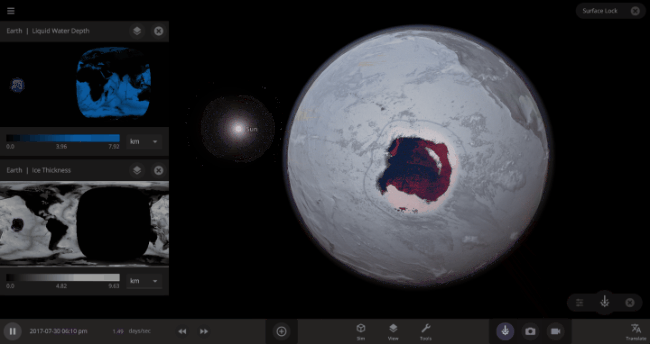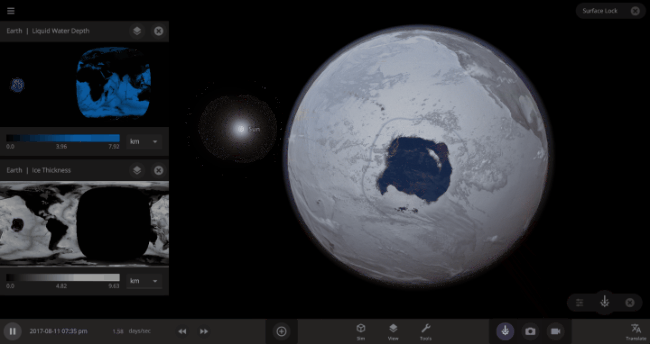
But you might have noticed that some of these phase changes take longer than you expect them to. If you’ve found yourself wondering “Why is it taking so long for the oceans to freeze?” or “I’ve been waiting for ages for the ice caps to melt, what’s going on??”, read on to learn more about the physics (and speed) of phase changes.

Energy Flow… Again

In ScienceLog #1, we explained how the flow of energy into and out of a planet will affect that planet’s temperature. In fact, the flow of energy also affects the phase of water.

As you know if you’ve ever boiled a pot of water, you need to add energy to turn water from a liquid to a gas. The opposite phase change— condensing water vapor into a liquid— involves the release of energy into the cooler environment surrounding the water. Similarly, energy needs to flow into a block of ice to melt it into water, but energy must flow out of a pool of water in order to turn it into ice. We can figure out how fast a phase change is occurring based on the speed at which energy is flowing into or out of the water.

The key point here is that phase changes are not instantaneous. You’ve probably already noticed that, if you pay attention to phase changes in your daily life: It can take a few days for snow to melt after a big blizzard, even if the temperature rises above freezing. Even ice doesn’t melt instantly in your drink on a hot day. And of course, we all know that water never boils as fast as we want it to, even if we set it on high heat.

The speed of a phase change of surface water in Universe Sandbox will depend on the temperature of the surface, the freezing or boiling point of water, and the mass of water that you’re trying to change. This last factor, the mass of the water, is probably the source of most of the confusion about this issue in Universe Sandbox. Since we’re all used to seeing phase changes in our everyday lives, we have some intuition for how fast we think they should happen. But the masses of the Earth’s ice caps or oceans are much, much larger than an ice cube or a kettle of water, and this significantly slows down the rate of boiling, melting, and any other phase change.

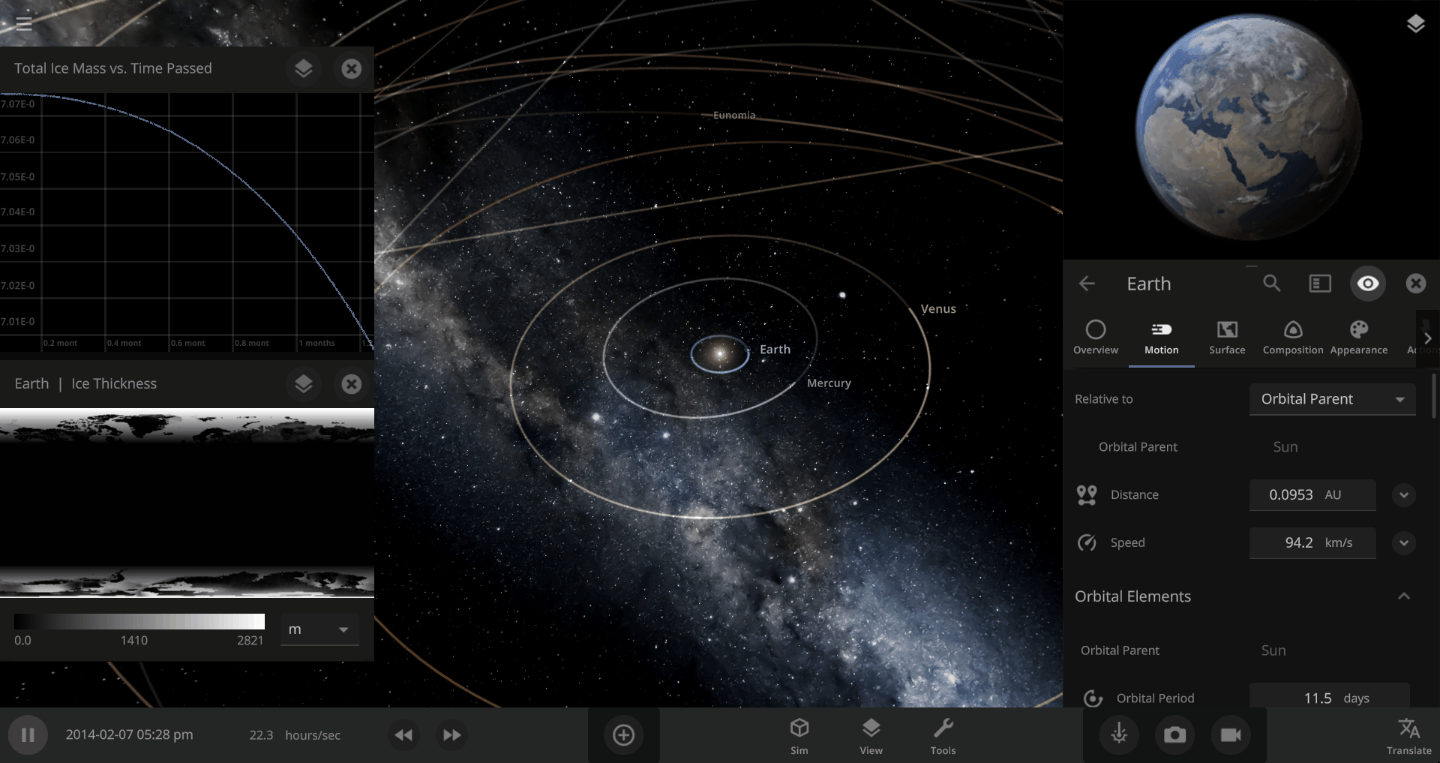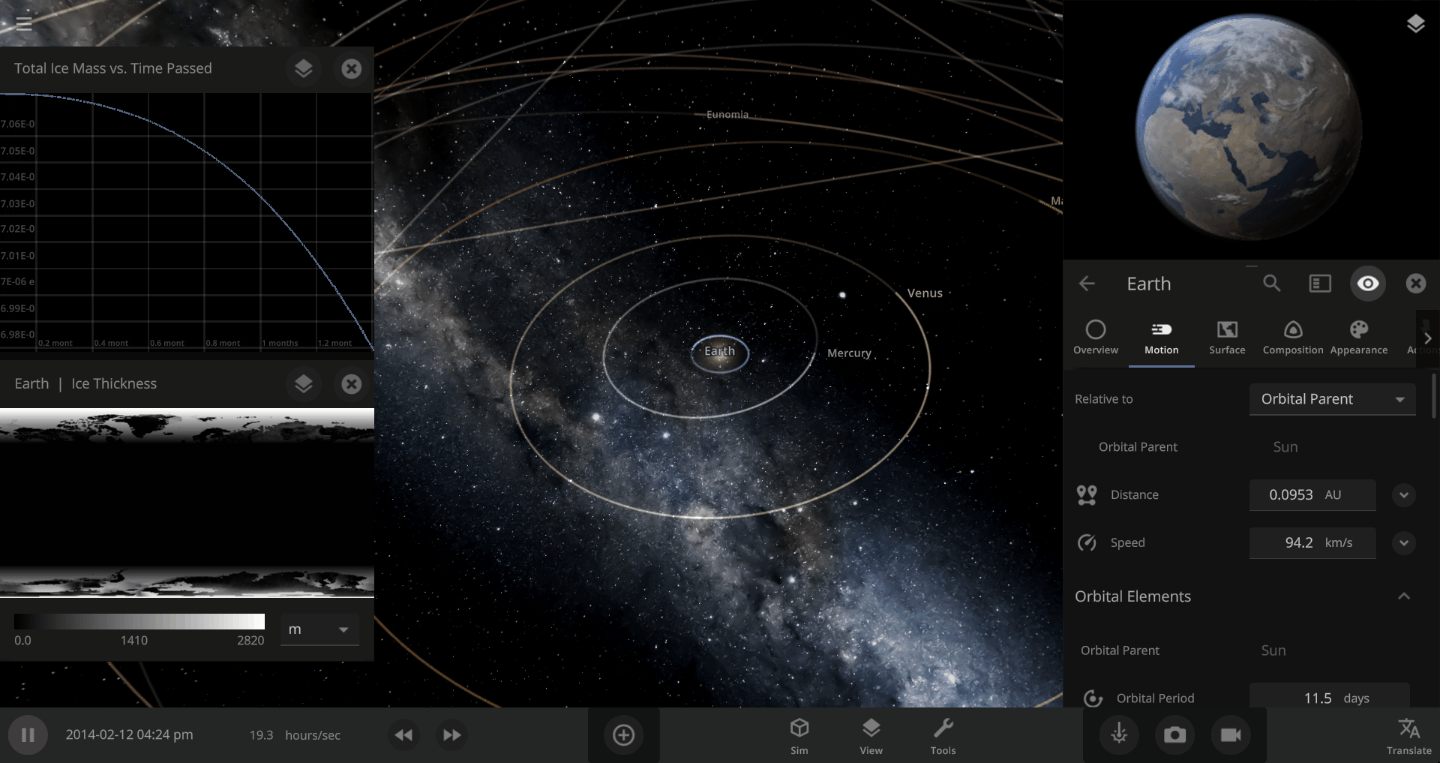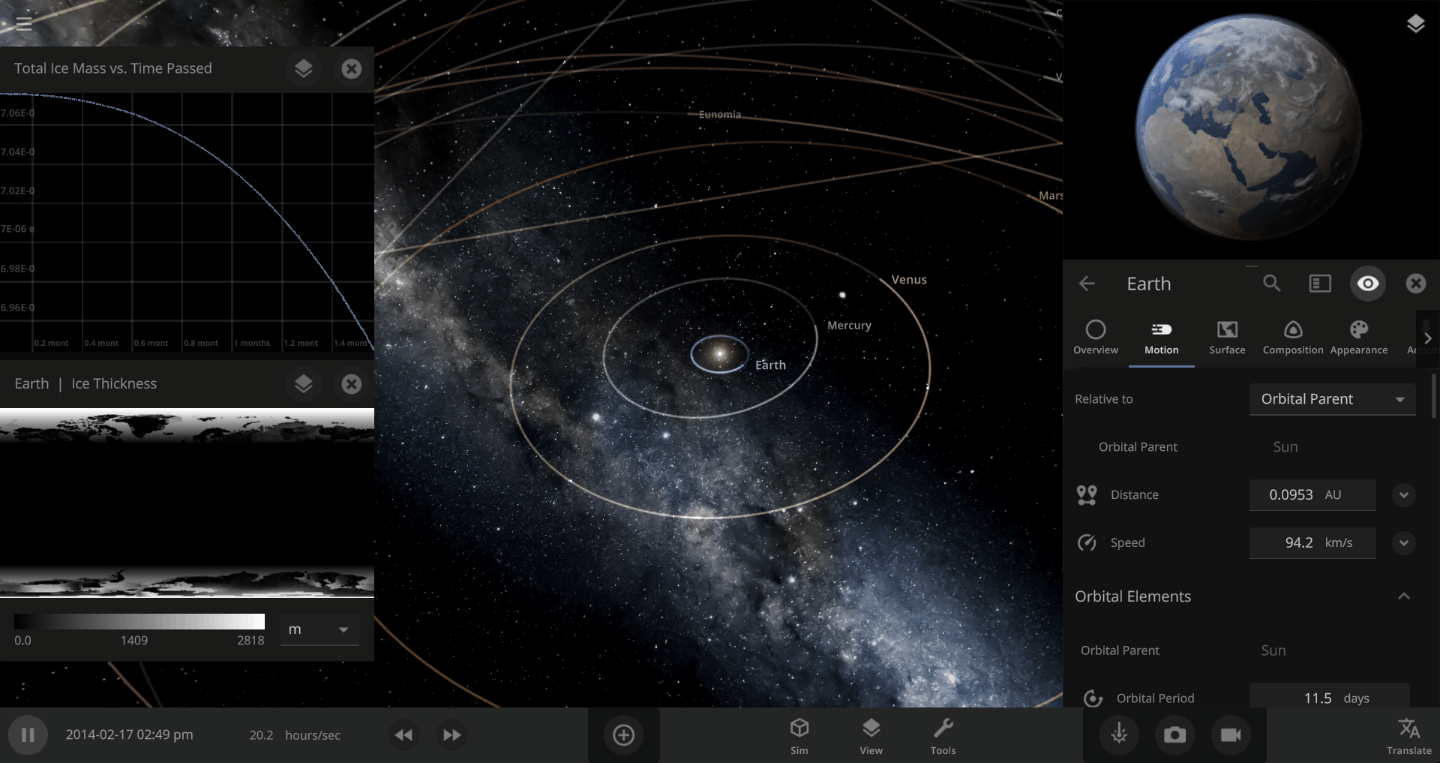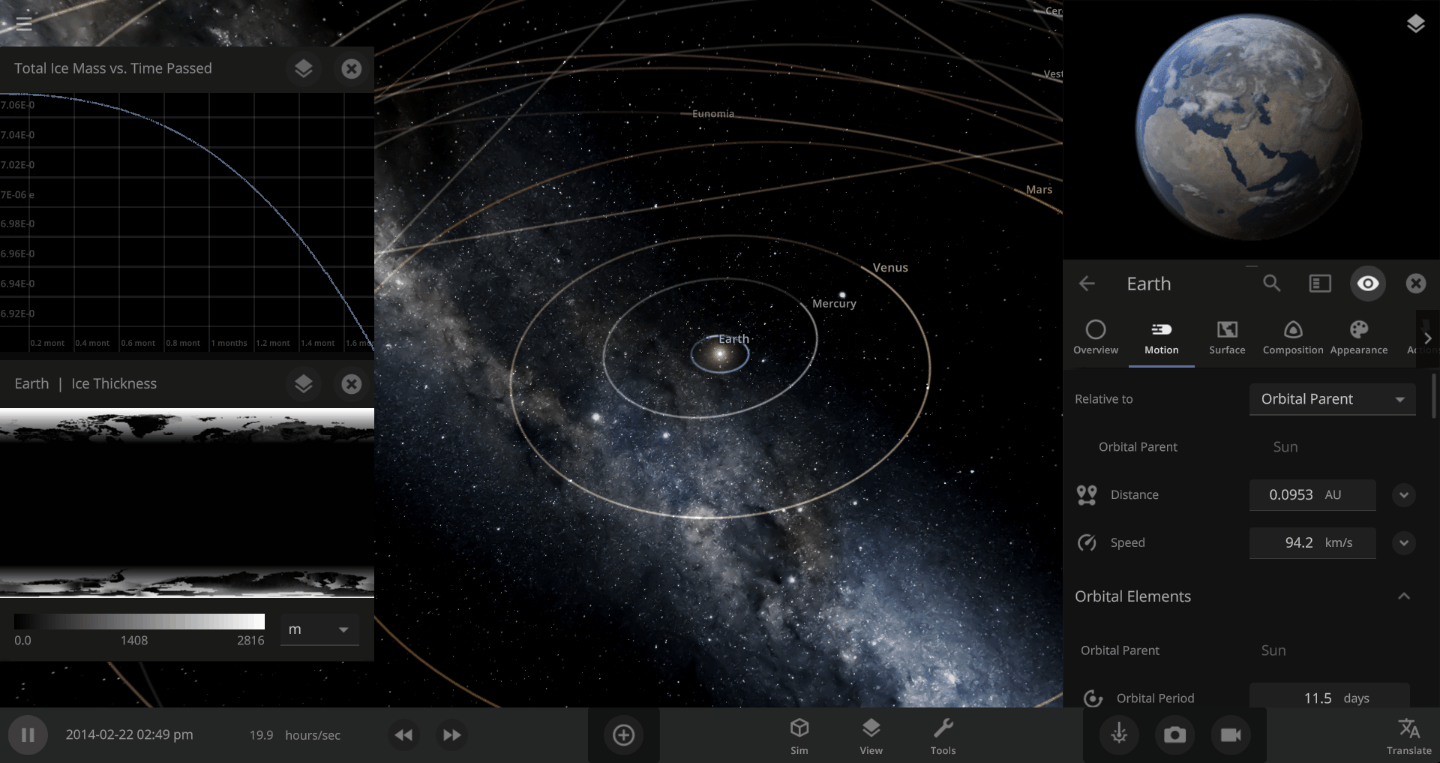
The heat from the too-close Sun is melting the Earth’s ice quickly, as you can see in the Total Ice Mass graph on the left, but not instantly.

That’s why you might have to wait a while for your simulated planet’s oceans to freeze or boil (depending on what you’ve done to that poor planet). Of course, if you get impatient, you can always use the new Stabilize Phases button in the Surface tab to instantly change the surface water to the correct phase based on the local temperature. What a convenient apocalypse!

…

…What’s that? You still don’t believe us that it would take a century to freeze the Earth’s oceans?

…

…You want some proof in the form of equations and hard numbers?

…

…All right, you asked for it. If you’re still with us, read on for the juicy, math-y details:

Bonus Math: How Long Does It Take to Freeze the Earth’s Oceans?

We’re going to put our money where our math is and walk through an example. Suppose we want to freeze all the water on Earth into ice. We could do this by deleting the Sun in the Solar System, although then we’d have to wait for the Earth to slowly cool down. If we’re impatient, we can skip ahead by just setting the Earth’s Average Surface Temperature to the lowest possible temperature: -273°C, or zero Kelvin (also known as “absolute zero”).

If you try this in Universe Sandbox, you’ll notice that after you change the temperature, the oceans are still made of liquid water. How long should we expect it to take to freeze all that water into ice: Days? Weeks? Months?

Let’s start by asking how much water we’re trying to freeze. Earth’s oceans have a mass of roughly 1.4 thousand billion billion kilograms. In scientific notation, that’s 1.4 x 10²¹ kg of water. To turn the liquid water into a solid, we need to remove energy from it. Since the water hasn’t frozen yet, its temperature is sitting at the freezing point, around 273 Kelvin. Since the Earth itself is at zero Kelvin, the heat energy in the water will flow into the Earth (and then out into space). 

Our next question is: How much energy needs to flow out of the water in order to freeze it? To answer this question, we use a property of water called the Heat of Fusion. This property represents how much energy, in Joules, is required to melt one kilogram of ice into water, or, conversely, how much energy must be removed to freeze one kilogram of water into ice. You can look up the Heat of Fusion for many different materials online— For water, it’s about 3.3 x 10⁵ Joules per kilogram.

This means that the amount of energy that must be removed from Earth’s oceans to freeze them entirely into water is:

\text{Energy} = \text{Mass} \times \text{Heat of Fusion} = (1.4 \times 10^{21} \text{kg}) \times (3.3 \times 10^5 \frac{\text{J}}{\text{kg}}) = 4.62 \times 10^{26} \text{J} 

That’s roughly the amount of energy that would be released by two billion Tsar Bomba hydrogen bombs, the most powerful nuclear weapon ever created.

Now we need to know the speed at which energy is flowing out of the water, and into its zero Kelvin environment. For this, we can use the Stefan-Boltzman law, which says that an object with temperature T will lose energy through its surface at a rate of 

\text{Rate} = \sigma T^{4}A

where σ, the Greek letter “sigma”, represents the Stefan-Boltzmann constant, and the A is the surface area of the object. 

The surface area of the Earth is about 5.1 x 10¹⁴ m², so the rate at which the oceans are losing energy is roughly

\text{Rate} = (5.7 \times 10^{-8} \frac{\text{J}}{\text{s m}^{2}~\text{K}^{4}}) \times (273~\text{K})^{4} \times (5.1 \times 10^{14}~\text{m}^{2}) = 1.61 \times 10^{17}~\text{J/s}

We can actually double-check this number in the game: First, put the Earth in an empty simulation. Then set Earth’s Average Surface Temperature to 273 Kelvin and look at the Energy Radiation Rate property. As expected, it shows that this Earth is losing energy at a rate of 1.61 x 10¹⁷ W (the Watts unit is equivalent to Joules per second). 

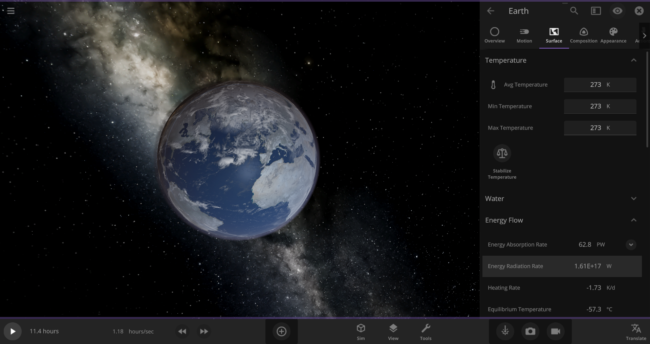
Back to our zero-Kelvin Earth: you probably know that only about 70% of our planet’s surface is covered in water. Since we’re only interested in how fast the oceans are losing heat, we should use a reduced rate of

\text{Rate} = 1.61 \times 10^{17}~\text{J/s} * 0.70 = 1.13 \times 10^{17}~\text{J/s}

We now know how much energy we need the oceans to lose in order to freeze them all, and how fast they are losing energy to their surroundings. Now we can easily calculate the time it will take for the oceans to lose the required amount of energy:

\text{Time} = \text{Energy / Rate} = (4.62 \times 10^{26}~\text{J}) / (1.13 \times 10^{17}~\text{J/s}) = 4.09 \times 10^{9}~\text{s}

There are about 3.15 x 10⁷ seconds in a year, so that’s

\text{Time} = (4.09 \times 10^{9}~\text{s}) / (3.15 \times 10^{7}~\text{s/yr}) = 132~\text{yr}

In other words, we estimate that it would take over 100 years(!) for the Earth’s oceans to completely freeze if the Earth’s temperature suddenly dropped to absolute zero. In real life, it would likely take even longer: The layer of ice that would form on top of the oceans would insulate the liquid water underneath, keeping it from freezing from much longer. Geothermal vents at the bottom of the oceans could also keep temperatures cozy for the microorganisms that live down there, possibly for billions of years.

If you’d rather go in the opposite direction and try to boil away Earth’s oceans by heating up the planet, you might find that it takes even more energy! That’s because the energy needed to change water from a liquid to a gas, known as the Heat of Vaporization, is almost ten times its Heat of Fusion. You can explore exactly this scenario in our Welcome | Part 2 guide, which you can find in Home > Guides > Tutorials. You can also learn more about how Universe Sandbox simulates the surface temperatures of objects in the Surface Simulation or the Energy & Heating tutorials.

Assumptions Addendum

Based on some comments we’ve received about the assumptions we made for this calculation, we wanted to go into a bit more depth about what they are, and why they may (or may not) be important. You’ll notice that because of these assumptions, the 132 years that we come up with really represents a minimum amount of time it would take for the oceans to freeze solid.

• Space is actually 3°K, not 0°K: 
  
  Yes, that’s true, the ambient temperature of empty space is around 2.7°K due to the cosmic microwave background. However, after the Sun disappears, the Earth is still much hotter than the temperature of space, and the difference between 0°K and 2.7°K is small, so this would not notably affect the speed of cooling.
  
  
• We didn’t consider atmospheric heating (the greenhouse effect):
  
  No we didn’t, though it is included in the Energy Absorption Rate in Universe Sandbox, so you can go see how large an effect this is by running the simulation for yourself! This effect actually makes the largest difference in the time it would take for the oceans to freeze. This Atmosphere Power is actually based on the infrared emissivity, ε, of Earth, a measure of how efficiently it emits infrared radiation. For Earth this is about 0.78 on a scale of 0-1 (1 being very efficient). The energy radiated back at Earth by the atmosphere is then calculated as:

P_{\rm{atm}} = \frac{\epsilon}{2}  \sigma T^4 A

where again σ, the Greek letter “sigma”, represents the Stefan-Boltzmann constant, and the A is the surface area of the object, and T is the temperature. Which works out to be 39% of the Energy Radiation Rate of Earth. So this means that the cooling rate is significantly slower when you take atmospheric heating into effect, adding another 83 years or so to the time it would take for Earth’s oceans to freeze solid.

• We didn’t discuss tidal forces:
  
  True, we did not discuss tidal forces, but they are also computed in Universe Sandbox as part of the Energy Absorption Rate. However, once you get rid of the Sun, the additional heating from tidal forces is over a million times smaller than the Energy Radiation Rate. The main source of tidal heating once the Sun is gone is the Moon, which adds about 2 terawatts of constant power (though it varies very slightly). This additional energy would only delay Earth’s oceans from freezing over for another day or so.
  
  
• We didn’t consider geothermal (internal) heating:
  
  Geothermal vents are mentioned in the last sentence of the second-to-last paragraph, but you’re right that we did not include them in our calculations. In fact, that property is not simulated in Universe Sandbox. However, assuming this rate is constant at providing 47 terawatts of power, this is still about 1000 times smaller than the Energy Radiation Rate, and would only add about 20 more days to the total time that it would take to freeze the Oceans.
  
  
• Earth is not a perfect blackbody:
  
  That’s also true. In many astronomical fields, celestial objects are approximated as blackbodies not only because it makes the math much easier, but also because we don’t know their exact emission and absorption properties, and it tends to be a pretty accurate approximation. This is why we approximate all of our objects as blackbodies to compute the Energy Radiation Rate in Universe Sandbox. Even though Earth is not a perfect blackbody,  the difference between it’s blackbody temperature and measured temperature is only a few degrees Celsius (not including the greenhouse effect).

Another assumption we made was that the surface temperature of the Earth would be starting at 0°K. As we mentioned, if we don’t start Earth at 0 °K, then we need to wait for it to cool off enough that it’s oceans would start to freeze, making it take even longer for Earth’s oceans to freeze solid. We dynamically compute the temperature of an object and its subsequent Energy Absorption and Radiation Rates in Universe Sandbox each second, so you can actually watch it cool in real time. Computing the exact amount of additional time this cooling would add is quite complicated. But we can run the simulation in Universe Sandbox and find that this will add another 100 years or so to the total time that it will take Earth’s oceans to freeze solid.

Since we do include atmospheric and tidal heating in Universe Sandbox, I encourage you to go and delete the Sun yourselves and see how long it takes for the oceans to freeze solid!

*So how long would you survive after the Sun disappeared? It would depend a lot on where you live and how much food you have on hand. The crops we depend on for food need sunlight to grow, although larger plants like trees can have enough energy stored to last for years without the Sun. Many people would probably freeze to death before they starved. Some people might last for a few months, especially those living in places like Yellowstone or Iceland with a lot of geothermal activity. After a few years, though, the Earth’s surface would grow so cold that the atmosphere would condense, and there’d be nothing left to breathe. It really makes you appreciate our nearest star, doesn’t it?

This blog post is part of our ongoing series of ScienceLog articles, intended to share the science behind some of Universe Sandbox’s most interesting features. If you would love to learn about the real-life science powering our simulator, please stay tuned and let us know what you would like to read about next.

To join our community discussions, please join us on our Steam Forum and our official Discord community.

Updated April 30, 2021